Tag: 3d

3D Statue of Liberty

I take aerial lidar point cloud and turn it into a 3D object.
https://www.thingiverse.com/thing:3615141

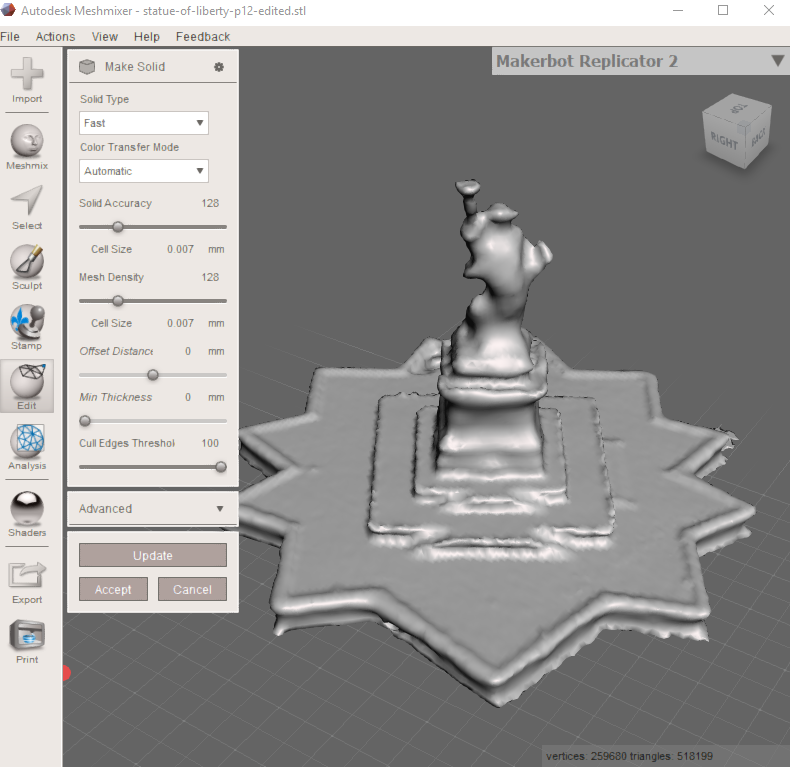
With Meshmixer, there is a great option in “Edit” > “Make Solid” and it generated this for me. Well done! Exactly what I was looking for. Otherwise it prints as hollow.

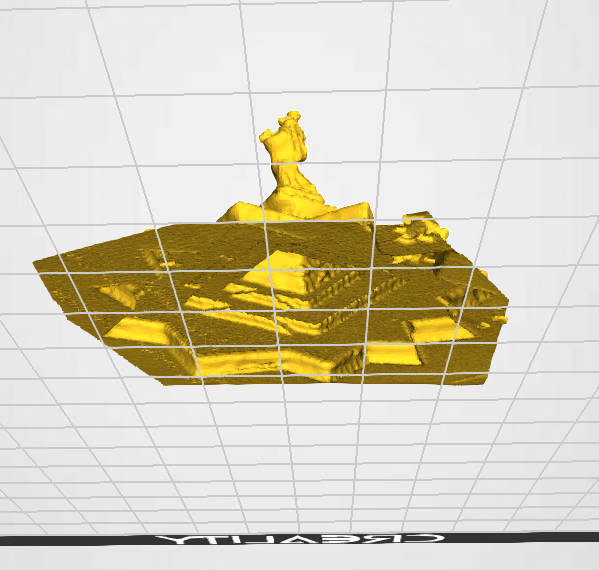
Have to fill in holes here

After some sculpting…

The Meshmixer tools are way more intuitive to use than Blender or anything else for that matter!

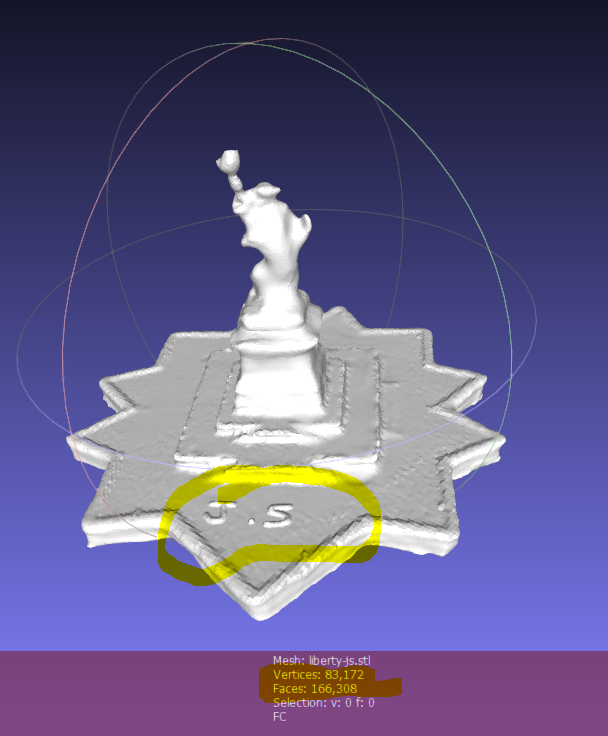
I didn’t notice but the bottom is not completely flat. As I printed this out. There was a power interruption when I used the pressure washer it jumped the breaker. Here’s the result.

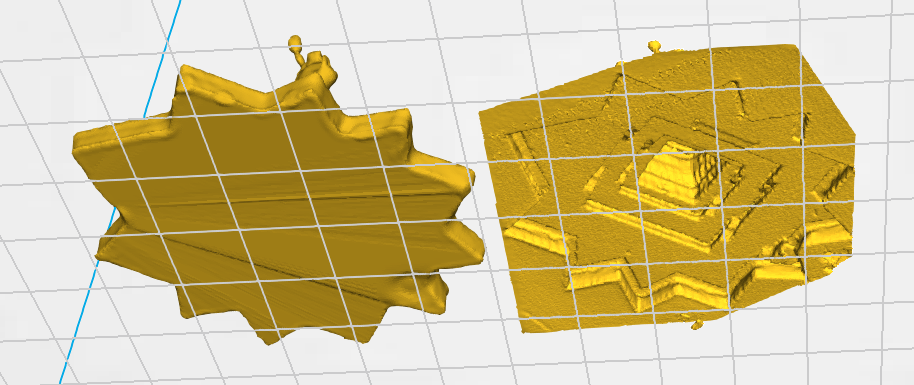
There are also too many polygons with the original. 83,172 Verticies and 166,308 Faces. Using MeshMixer I could reduce verticies to 21,141 and faces 42,282. This lower poly count object should print cleaner too. Notice the surface.

Obviously the wood print failed. But I am happy with the white result!

Space Filling Curves vs. Octree

Octree

An octree is a tree data structure in which each internal node has exactly eight children. Octrees are most often used to partition a three-dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional analog of quadtrees.

We humans mostly deal with low dimensional data, so we give this type of structure some names:

  • 1-D data: binary tree
  • 2-D data: quadtree
  • 3-D data: octree
  • K-D data: k-d tree, or k-dimensional tree, is a data structure used in computer science for organizing some number of points in a space with k dimensions.

These are all tree-like data structures, which are very useful for range and nearest neighbor searches.

Octree example

Space Filling Curves

Space filling curves refers to a class of functions that k dimensional data to 1 dimension.

Meaning a class of functions that can map k-dimensional data into a single number n

f(n_1, n_2, …, n_k) -> n

The caveat is there is a restriction on the number it maps, i.e. n_1, as space filling curves are a fractal functions, it cannot be extended to the reals, but rather to the binary fractions (a subset of the rationals). This lets you get arbitrarily close to any number you want (and cover all the IEEE floating points).

Class of functions means that there are many functions that can be considered a space filling curve. Common to use Hibert and Z-order.

Visualization of a 3D space filling curve may look like with a Hilbert curve function.

Compare and contrast

There are certain optimal use cases for each of these.

  • Trees have the benefit being able to limit the depth of your queries, which makes it especially useful in computer graphics so you can stop querying for points that you don’t need.
  • Space filling curves have the benefit of modify data faster, because the location to store that data can be calculated. Because trees have the cost of potentially rebalancing subtrees and creating/updating/deleting.

Other structures?

There are some variants on structures for storing multi-dimensional data.

R-Tree

It’s yet another type of tree.

Visualization of an R*-tree for 3D points using ELKI.Hilbert R-Tree is a variant on the R-Tree to achieve better performance.

Data Stores

I won’t go in too much detail because this is out of scope, but in programming there are databases and data stores which can handle large amount of high dimensional data.

First, a distinction. A database can handle complex queries. A data store can be dumber, simple storage format and won’t handle things like transaction for you.

An analogy could be like “database is like an accountant, who you can ask for certain data and operations, such as ‘give me all last year’s data for people with last names in T'”, whereas “data store is like a library and you have to go find and collect that data yourself, but it’s stored in an organized fashion”.